¿Hemos llegado al límite del conocimiento?
Los matemáticos afirman que las ecuaciones matemáticas son bellas, o al menos deberían serlo. Pero ¿qué significa que una ecuación matemática sea bella?
Pongamos un ejemplo con las Ecuaciones de Campo de la Relatividad General:
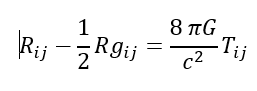
¿Qué ven los matemáticos y físicos en este conjunto de símbolos para afirmar que es bella y quizás otra ecuación con más términos no lo es?
A continuación, podemos ver la famosa ecuación de Euler. Los matemáticos se asombran de que exista una ecuación que relacione cinco de los números mas famosos e importantes de la matemática; e, i, π, 0 y el 1.
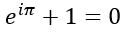
Estas dos ecuaciones forman parte del Código del Universo. Mírelas detenidamente y verá – como en la película Matrix -, la obra del arquitecto de nuestro Mundo. Somo la creación de un Dios Matemático.

La Naturaleza tiende a las explicaciones más simples posibles aplicando el Principio de la Navaja de Occam. El principio de la Navaja de Occan viene a decir que cuanto más simple sea una explicación mejor. Eliminemos lo superfluo. Pero ¿cómo se mide la simplicidad? ¿Cuándo una ley física o matemática es simple?
Kurt Gödel fue un lógico-matemático de origen austríaco que revolucionó la ciencia del conocimiento o epistemología. Fue capaz de demostrar matemáticamente que el conocimiento lógico-matemático tiene un límite y nunca se podrá llegar a demostrar todo mediante procedimientos matemáticos. Las matemáticas se autolimitan.
Lo hizo con sus dos famosos teoremas: el Teorema de la Indecibilidad y el Teorema de la Incompletitud.

El Teorema de Indecibilidad asevera: En todo sistema axiomático lo suficientemente amplio como para incluir a la teoría de números siempre existirán afirmaciones indecidibles, es decir, que no se puede demostrar si son falsas o verdaderas.
